Pore network modeling prospects, towards predictive models

The pore network model (PNM) that we developed is an effective computational model for simulating the performance of porous electrodes for a wide variety of operating conditions. As the real electrode can be translated to a pore network, the electrode microstructure can be correlated to the performance, and structure-performance relationships can be elucidated to guide the design of novel porous electrodes for electrochemical applications. Although effective, the PNM can be further improved to better capture the electrode performance. In this post, possible extensions of the model are provided, of which some are currently being explored and therefore discussed in more detail. By developing a computational modeling framework, we aim to speed up the understanding and design of electrodes for electrochemical applications, with a focus on redox flow batteries. Hence, by collaborating and sharing our research we can make a greater impact on society. Therefore, the pore network model with several extensions is available on GitHub (see ‘Open-source codes’).

Possible research directions for extending the modeling framework include:

(1) The extension of the PNM to model a full non-symmetric redox flow battery to simulate charge-discharge cycles. To this end, multiple extensions must be made to the model including the addition of species migration, species crossover, and charged membranes. The first step is the extension of the advection-diffusion-reaction equation to the full Nernst-Planck equation to include species migration. In the current model, the low species concentration and high background electrolyte concentration make the assumption of negligible migration applicable [1]. Combined with the single-electrolyte configuration and without the simulation of a charged membrane, the performance of the flow cells can be well-described. However, for systems operating at higher species concentration, with full-cell configurations, and/or with charged membranes, species migration must be considered. A good starting point for the proposed extension is the publication of Agnaou et al. where they added the Nernst-Planck equation in OpenPNM [2]. Furthermore, the model could be extended to include charged membranes. The current framework accounts for the membrane by considering the membrane resistance using Ohm’s law. Whilst being a reasonable assumption for single-electrolyte configurations, it cannot be translated to full-cell designs as species crossover should be considered. Furthermore, for charged membranes, the charged groups, electro-osmosis, and species migration should be taken into account. A starting point is the paper of Aghighi et al. where they simulated a full fuel cell membrane-electrode-assembly using a PNM [3].

(2) Incorporating temperature effects in the modeling framework. We observed that, during flow cell operation, the temperature increase in the electrolyte tanks for our single-electrolyte 2.55 cm2 flow cells could be as high as 5 °C, indicating an even higher temperature increase in the reactor. With electrolyte conductivity experiments it was found that the conductivity of the non-aqueous TEMPO-based electrolyte strongly changed with temperature, significantly impacting the battery performance as the conductivity is a performance-limiting parameter for TEMPO electrolytes. The increase in ionic conductivity with temperature was studied by Zhang et al. for NaCl and CaCl2 in propylene carbonate and water for which they derived an equation relating the ionic conductivity to the temperature and electrolyte concentration, originating from the correlations between the conductivity and mobility, and mobility and ionic strength [4]. To incorporate such a relation between temperature and ionic conductivity, the PNM should take into account reactor (overpotential losses) and pump heating. Several thermal models exist and could be used for inspiration, including the work of Ren et al. [5].

(3) A more accurate computation of the pressure drop in the pore network. The fluid transport dictates the mass transport characteristics and pressure drop and should be properly defined. The developed PNM describes the pore pressure by the Hagen-Poiseuille equation, where the pressure drop over the throats is defined by the hydraulic conductance of the cylindrical throat connecting pore i and j, and the pressure drop over the pores is defined using shape factors. However, besides the throat constriction factor, throat expansion and contraction should be considered [6, 7]. To this end, we extended the PNM to include throat expansion and contraction in the pressure drop definition. 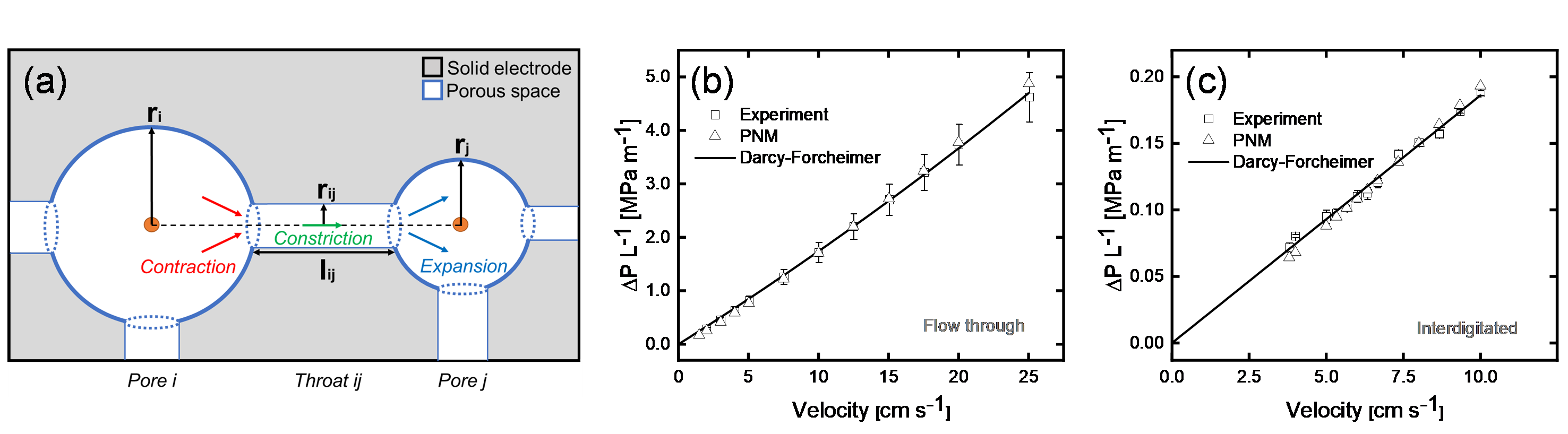Figure 1: (a) Schematic representation of the spheres and cylinders representing the pores and throats in the pore network model, together with the pore and throat radius, throat length, and the visualization of throat contraction, constriction, and expansion. (b-c) Pressure drop per electrode length over a range of superficial velocities showing the experimental data, Darcy-Forchheimer fits, and pore network model fitting results for the: (b) flow-through flow field, and (c) interdigitated flow field.

(4) The addition of a velocity-dependent mass transfer coefficient. The current mass transfer coefficient definition relies on the film theory in which the film layer is assumed equal to the pore radius in every pore. Hence, the mass transfer coefficient only varies with the diffusion coefficient and pore diameter and is thus velocity independent. The relation can be improved by applying a velocity-dependent mass transfer coefficient correlation defined by dimensionless parameters [8], which we, therefore, included in the model. 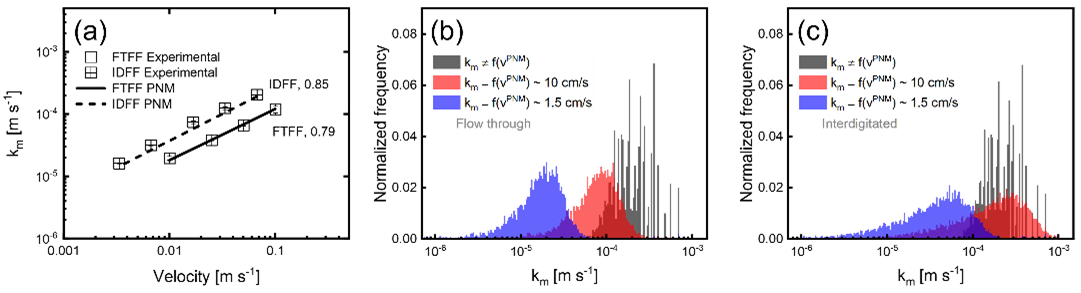Figure 2: (a) The global mass transfer coefficient relationship obtained experimentally and by fitting the pore network model to the experimental results over a range of superficial inlet velocities, for the flow-through and interdigitated flow fields, plotted on a double-log scale. (b-c) Histograms with the normalized frequency of the velocity-independent and dependent local mass transfer coefficients at the pores of the pore network model for inlet velocities of 10 and 1.5 cm s-1 for (b) the flow-through flow field, and (c) the interdigitated flow field.

(5) Extending the PNM to simulate multiphase flow to account for hydrogen evolution and incomplete wetting of the porous structure. The current model only relies on all-liquid transport and thus omits gas transport. Therefore, the model could overpredict the flow cell performance as, for certain chemistries and operating conditions, incomplete wetting and hydrogen evolution can impact the performance in experimental conditions. Pore network models for multiphase flow exist in great amounts in the literature and include the work of Aghighi et al. on fuel cells [9, 10].

(6) Simulating a wide variety of flow field designs, including flow-by and hybrid flow field geometries. To date, the RFB performance with flow-by and hybrid flow geometries is generally simulated with volume-averaged computational fluid dynamic simulations [11, 12–16], without considering the electrode pore structure. Complex flow field designs should be incorporated into pore-scale simulations, for example into PNMs as they are computationally light, to investigate the effect of the fluid flow induced by the flow field on the local performance in the electrode. In the current PNM, the boundary conditions determine the flow field, which is inaccurate or impractical for flow-by or hybrid designs. Therefore, we propose the coupling of pore network models with computational fluid dynamic simulations to simulate the flow field channels, intending to extend the knowledge on flow field-electrode interactions [17]. Therefore, to model a variety of flow field designs, we started the coupling of the PNM to a continuum model that accurately describes the fluid flow in parallel flow field design, inspired by the work of Weishaupt et al. [17]. 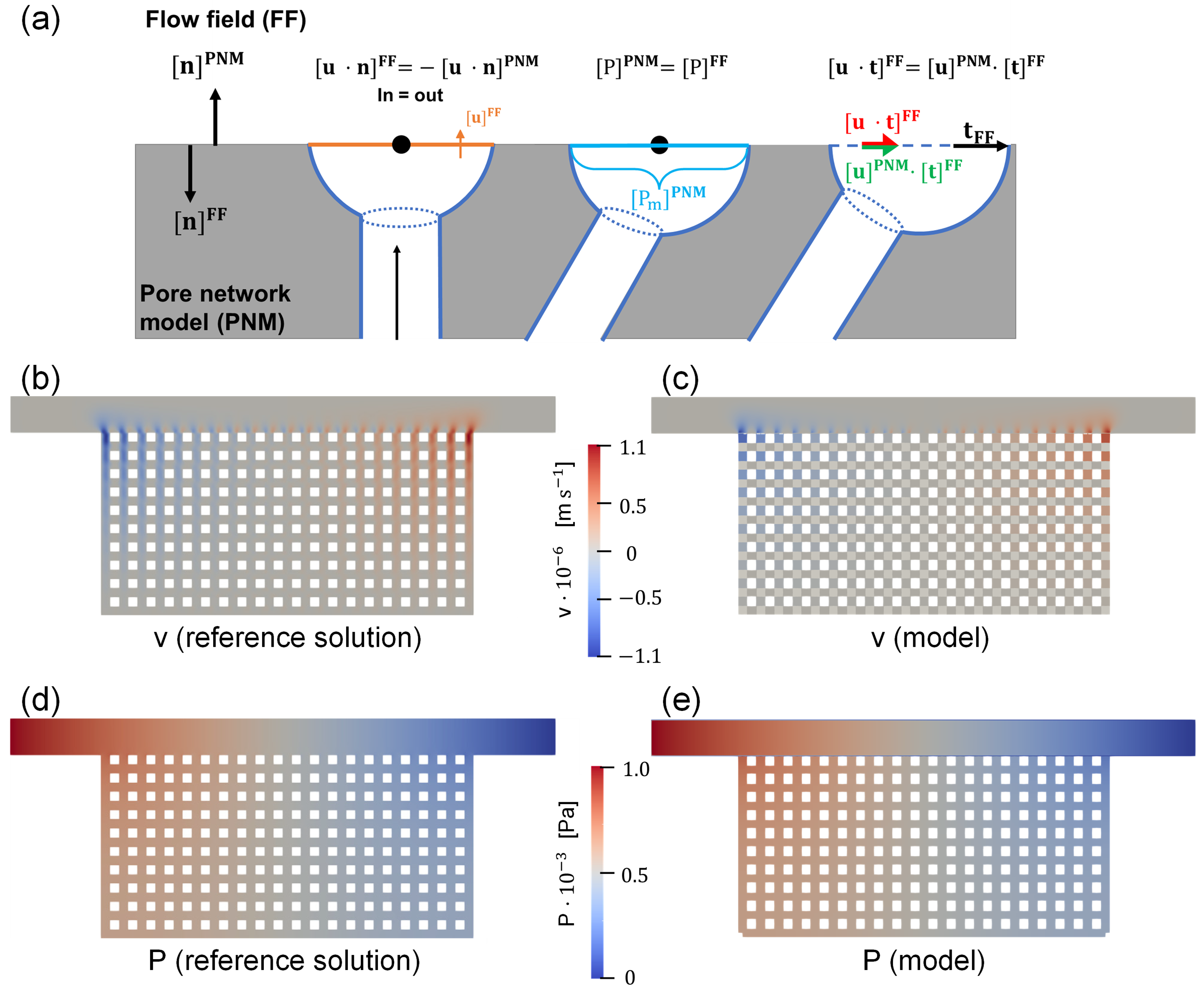Figure 3: (a) Schematic of the continuum model and pore network model coupling conditions. The left pore represents the mass conservation coupling condition, the middle pore the continuity of pressure across the coupling interface for the normal momentum component, and the right pore the conservation of the tangential momentum component. (b-e) Qualitative comparison of the continuum model and pore network model coupling with the reference solution from [17] (b,c) for the normal velocity component (d,e) and pressure.

(7) The coupling of the PNM with other modeling frameworks to increase the model accuracy. The benefit of coupling modeling frameworks is that the advantages of both could be combined to obtain a modeling framework with a low computational cost and high accuracy. For example, the PNM could be coupled to pore-level models that can simulate surface roughness and incomplete pore wetting of individual pores, or to computational fluid dynamic models that can better capture the fluid flow through the electrode. By combining pore-level models with the PNM, the trends at the pore-level could be translated to the overall pore structure to decrease the computational cost of the modeling framework, compared to simulating the entire electrode using detailed pore-level models, which is computationally expensive [18].

(8) The use of the PNM to aid in the design of advanced electrode structures. The PNM is useful for investigating the transport properties in porous electrodes, which could aid in assessing the electrode performance for a range of operating conditions, electrolyte solutions, and flow field geometries. To this end, with the model developed two novel non-solved induced phase-separated electrodes were analyzed with the PNM (Figure 4), a NIPS with macrovoids (the DMF - 0.20g/mL - 21 °C developed by Jacquemond et al. [19]) and a porosity gradient NIPS (developed by Wan et al. [20]). The performances of both electrodes were evaluated with the TEMPO/TEMPO+ electrolyte with low electrolyte conductivity and facile kinetics, and with the VO2+/VO2+ electrolyte with high conductivity but sluggish kinetics. Furthermore, the flow-through and interdigitated flow fields were analyzed and the resulting polarization curves can be found in Figure 4c.

Several performance trends can be obtained from the PNM simulations, including: (1) the porosity gradient electrode outperforms the electrode with macrovoids in terms of the electrochemical performance for all configurations. The effect is most prominent for the vanadium electrolyte with sluggish kinetics because of the significant decrease in the activation overpotential with the porosity gradient electrode due to the high internal surface area. (2) The porosity gradient electrode features a significantly higher pressure drop compared to the electrode with macrovoids, resulting in a higher pumping power requirement, which is especially detrimental for flow-through flow configurations. (3) The electrode with macrovoids features electrolyte transport pathways as a result of the macrovoids (Figure 4a), leading to convection and diffusion transport-dominated domains. These domains dictate the electrochemical performance by the formation of local reaction zones besides convective electrolyte transport domains, see Figure 4d. (4) The porosity gradient electrode has a uniform in-plane electrolyte distribution with the flow-through flow field and follows the path-of-least-resistance with the interdigitated design, resulting in high convection over the rib and local reaction zones above the channels, near the membrane (Figure 4b,e). (5) The vanadium electrolyte results in a higher current output at elevated potentials due to the greater utilization of the available internal surface area at the investigated electrolyte velocity, because of the higher electrolyte conductivity compared to the TEMPO electrolyte (Figure 4e-f).

Based on the presented study, I advise using the porosity gradient electrode in combination with interdigitated flow designs and with electrolytes with high ionic conductivity. On the contrary, the electrode with macrovoids could be used in combination with flow-through flow fields and kinetically facile electrolytes. A PNM assessment, such as the brief analysis presented here, can guide electrode and system design, which could save valuable time and experimental resources.

Figure 4: Preliminary results of pore network model simulations of novel non-solvent induced phase-separated electrodes: (a,d) with macrovoids [19], and (b,e-f) with a porosity gradient [20]. (a b) The absolute velocity profiles through the throats in the electrode for the vanadium chemistry, with an interdigitated flow field, and evaluated at 8 cm s-1. (c) Polarization curves for all tested systems: 2 electrode types (with macrovoids and a porosity gradient), 2 flow field designs (flow-through and interdigitated), and 2 chemistries (vanadium and TEMPO). (d-f) Concentration profiles through the electrode with the interdigitated flow field, evaluated at 8 cm s-1 and 1 V overpotential, for: (d-e) the vanadium chemistry, and (f) the TEMPO chemistry. The electrodes have different scale bars because of the difference in electrode size (due to network extraction RAM issues for the porosity gradient (a large number of pores)), hence, both electrodes have a different channel and rib distance.

(9) A better geometrical representation of the porous structure. One possible extension would be to include compressed electrode structures by obtaining the X-ray tomograms under compression using a similar set-up as used by Tenny et al. [21]. By including compressed electrodes in the PNM, the experiments can be conducted under compression, as is desired for industrial applications, resulting in minimal contact resistances and thus minimal ohmic corrections during model validation [22]. Furthermore, pore and throat geometrical definitions beyond spheres and cylinders could be integrated to better translate the electrode structure to a pore network. Although spheres and cylinders are a reasonable assumption for the pore space in many commercial fibrous electrodes, it is an oversimplification and could be inaccurate for more complex electrode structures such as woven electrodes [23]. To this end, it is worth investigating various geometrical definitions of the pore space. OpenPNM has several built-in geometrical definitions including cones and cylinders, pyramids and cuboids, and cubes and cuboids. For example, Misaghian et al. used pyramids to represent the pore space of a randomly organized fibrous material with a binder [8]. Yet, such geometrical definitions could still underestimate the complex space in porous electrodes as surface roughness is complex to include, for which additional correction factors must be considered.

(10) Finally, the extension of the PNM to model other electrochemical technologies by adopting multiphase flow and by adjusting the reaction terms in the model. Various PNMs already exist for fuel cells, but pore network models for complex hybrid batteries (e.g., iron plating, iron-air) or CO2-electrolysis could be viable options to explore.

References:
[1] A. J. Bard, L. R. Faulkner, Electrochemical methods (John Wiley & Sons, New York, Second., 2001).
[2] M. Agnaou, M. A. Sadeghi, T. G. Tranter, J. Gostick, Comput. Geosci. 140, 104505 (2020).
[3] M. Aghighi, M. A. Hoeh, W. Lehnert, G. Merle, J. Gostick, J. Electrochem. Soc. 163, F384–F392 (2016).
[4] W. Zhang, X. Chen, Y. Wang, L. Wu, Y. Hu, ACS Omega. 5, 22465–22474 (2020).
[5] J. Ren et al., Int. J. Heat Mass Transf. 192, 122926 (2022).
[6] A. Fathiganjehlou et al., Chem. Eng. Sci. 273, 118626 (2023).
[7] F. Larachi et al., Chem. Eng. J. 240, 290–306 (2014).
[8] N. Misaghian, M. A. Sadeghi, K. Lee, E. Roberts, J. Gostick, J. Electrochem. Soc. 170, 070520 (2023).
[9] M. Aghighi, J. Gostick, J. Appl. Electrochem. 47, 1323–1338 (2017).
[10] M. Aghighi, M. A. Hoeh, W. Lehnert, G. Merle, J. Gostick, J. Electrochem. Soc. 163, F384–F392 (2016).
[11] J. D. Milshtein et al., J. Electrochem. Soc. 164, E3265–E3275 (2017).
[12] V. Muñoz-Perales, M. van der Heijden, P. Á. García-Salaberri, M. Vera, A. Forner-Cuenca, ACS Sustain. Chem. Eng., 11 (33), 12243-12255 (2023).
[13] M. Messaggi et al., Appl. Energy. 228, 1057–1070 (2018).
[14] M. Macdonald, R. M. Darling, AIChE J. 65, 1–11 (2019).
[15] C. H. Chen, K. Yaji, S. Yamasaki, S. Tsushima, K. Fujita, J. Energy Storage. 26, 100990 (2019).
[16] Q. Xu, T. S. Zhao, P. K. Leung, Appl. Energy. 105, 47–56 (2013).
[17] K. Weishaupt, V. Joekar-Niasar, R. Helmig, J. Comput. Phys. X. 1, 100011 (2019).
[18] J. Zhao, F. Qin, D. Derome, Q. Kang, J. Carmeliet, Adv. Water Resour. 145, 103738 (2020).
[19] R. R. Jacquemond et al., Cell Reports Phys. Sci. 3, 100943 (2022).
[20] C. T. C. Wan, R. R. Jacquemond, Y. M. Chiang, A. Forner-Cuenca, F. R. Brushett, Energy Technol. 11, 2300137 (2023).
[21] K. M. Tenny et al., Energy Technol. 10, 2101162 (2022).
[22] V. Muñoz-Perales et al., ChemRxiv (2023), doi:10.26434/chemrxiv-2023-n2mmd.
[23] M. van der Heijden, R. van Gorp, M. A. Sadeghi, J. Gostick, A. Forner-Cuenca, J. Electrochem. Soc. 169, 040505 (2022).