Computational optimization strategies for electrode design

Modeling strategies have the potential to enable the bottom-up design of reactor components through optimization strategies. The rapid rise in computational power has driven the increasing interest in optimization methods for a wide range of applications, including electrochemical technologies. The optimization of the electrode structure is of special interest because of a range of contracting requirements that motivate computational work, i.e., high electrochemical surface area, facile mass transport, and low pressure drop.

An example of a taxonomy of optimization methods is provided in Figure 1, showing a wide variety of optimization classifications. The optimization method of choice depends on the optimization problem, as no optimization method is a clear winner to all kinds of problems, and depends on the complexity of the problem, the objective function, the constraints, and the number of variables and unknowns [1]. To define which optimization category is suited for the application, the problem type needs to be defined. In Figure 1 an example is provided of a workflow that can be followed to determine the appropriate optimization method. First, it needs to be determined whether the problem is discrete or continuous. In discrete optimization problems, the problem variables adopt values of a discrete set, often a subset of integers, and can be further divided into exact (often used to provide optimal solutions for smaller problems [1]) and approximate methods, of which the latter is used to find close-to-optimal solutions for complex optimization problems in a short time period [2]. In continuous optimization problems, the values can have any real value and can be subdivided into nonlinear and linear programming [3]. The nonlinear programming branch can be further divided into global and local search methods, of which the global method can be split into heuristic, random search, and meta-heuristic methods. In heuristic methods, the optimization determines an optimal solution by iteratively improving the candidate solutions concerning a given problem. In random search methods, the gradient of the problem does not need to be optimized and thus relies solely on random sampling of solutions near the problem. Meta-heuristic methods are similar to heuristic methods; however, the algorithm used is generic and can deal with multiple problems [4]. The meta-heuristic methods comprise single-solution or population-based optimizations, in which the latter is divided into evolutionary and swarm intelligence algorithms. Swarm intelligence algorithms are based on studied interactions by living organisms (e.g., birds, fish, ants) by enhancing the objective function, or fitness function, by self-organization with a limited number of restrictions towards a global optimum [2]. Evolutionary algorithms, on the other hand, are based on the principle of natural evolution of a solution set over generations using operators based on diversity and selection. They can handle complex optimization problems with many variables and constraints, making evolutionary algorithms promising for the optimization of electrodes for electrochemical devices with complex performance trade-offs.

Artificial intelligence emerged in the mid-1950s inspired by Alan Turing and is gaining an increased interest in battery research to solve complex multivariable problems. Especially the machine learning branch is of interest which is capable to evaluate multidimensional datasets, discover data patterns, and can unlock applications that are difficult to exploit otherwise [5]. Both population-based algorithms mentioned above are unsupervised search-based machine learning algorithms that optimize for the global maxima and do not require training data, which for example is necessary when using neural networks as a machine learning strategy. Though, these population-based algorithms do not guarantee an optimal solution [6]. Evolutionary algorithms are a rapidly growing area of artificial intelligence, whereas swarm intelligence has only recently been applied and is thus still in the beginning stage [6].

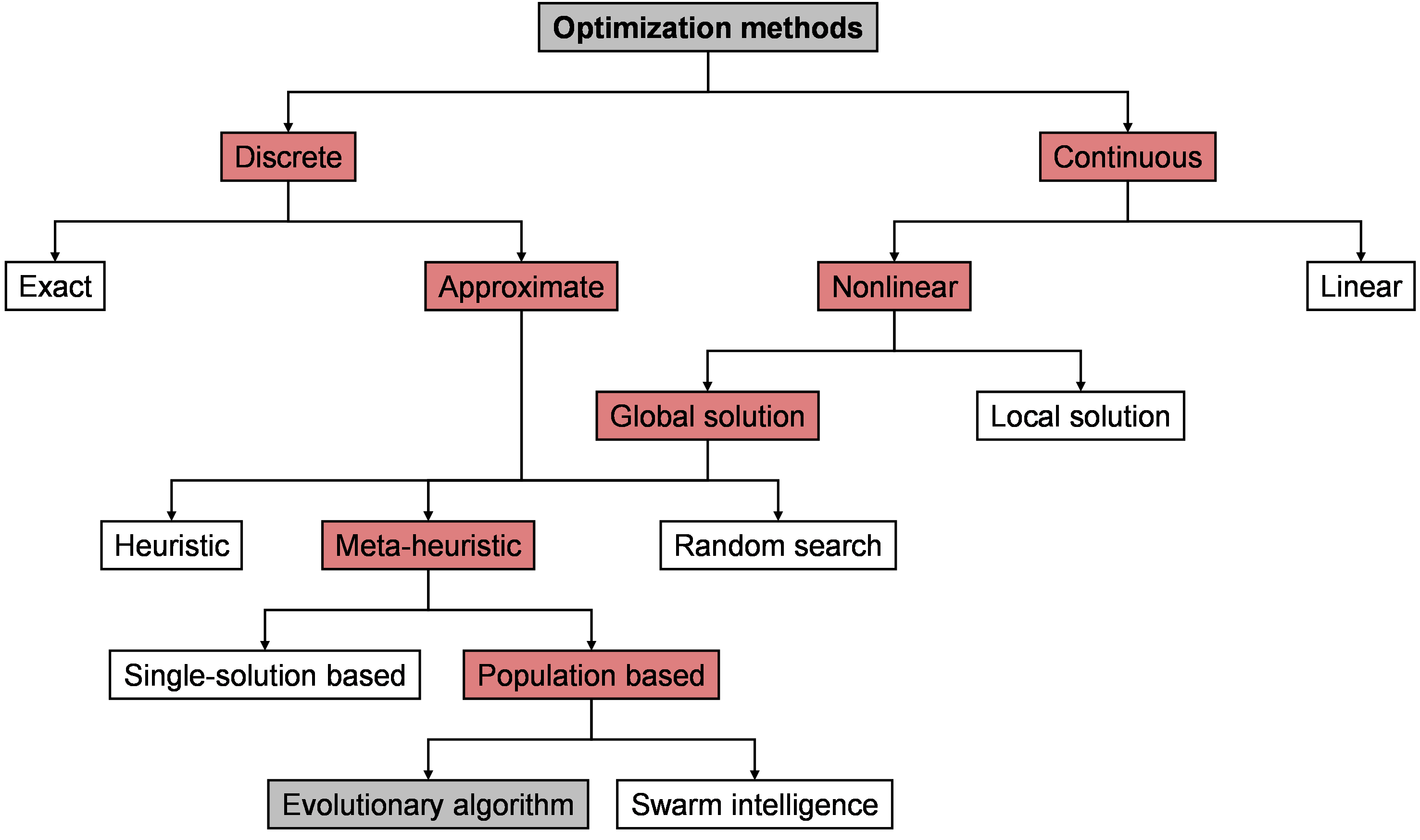Figure 1: Taxonomy of optimization methods, with the evolutionary algorithm optimization method highlighted, modified from [1].

References:
[1] M. Janga Reddy, D. Nagesh Kumar, H2Open J. 3, 135–188 (2020).
[2] M. Koopialipoor, A. Noorbakhsh, in Emerging Trends in Mechatronics, A. Azizi, Ed. (IntechOpen, 2020), p. 30.
[3] S. Wright, Found. Comput. Process Des., 1–14 (1999).
[4] Vinicius Fulber-Garcia, Heuristics vs. Meta-Heuristics vs. Probabilistic Algorithms. Baeldung (2023), (available at https://www.baeldung.com/cs/heuristics-vs-meta-heuristics-vs-probabilistic-algorithms).
[5] T. Lombardo et al., Chem. Rev. 122, 10899–10969 (2022).
[6] K. Thoiba Meetei, Int. J. Sci. Res. 3, 231–235 (2014).